Experiments on bulk crystals

Over the years we have conducted many fruitful experiments on bulk crystals grown by collaborators at Princeton (Cava and Schoop, Dept. of Chemistry) and from all over the world. Here are some recent highlights on electronic transport studies in bulk crystals:

N. Quirk, et al. Singular angular magnetoresistance and sharp resonant features in a high-mobility metal with open orbits, ReO₃. Physical Review Materials 5, 105004 (2021).
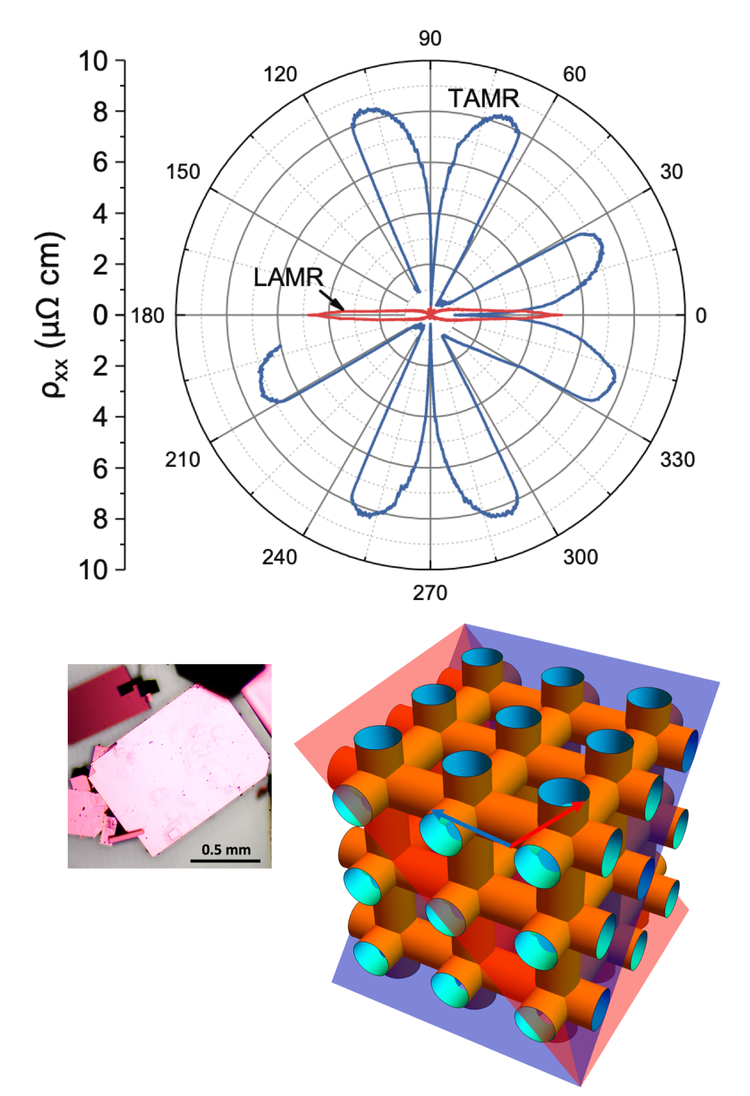
- In this study we found that the magnetoresistance in the highly conductive transition-metal oxide ReO₃ has an extreme singular dependence on the angle of the applied magnetic field. When the field is tilted out of the a-b plane, the magnetoresistance at 9 T changes by more than 100,000%. It increases if tilted in the transverse plane, but decreases if tilted in the plane parallel with the current. We found that this effect is caused by the very high carrier mobility and atypical Fermi surface, which is comprised of a grid of cylinders intersecting at right angles.

ReO3 AMR — Upper: The transverse (TAMR) and longitudinal (LAMR) angular magnetoresistance at B = 9 T and T = 1.8 K in single-crystal ReO3. The sharp differences in the AMR are due to open electron orbits on a multiply connected Fermi surface. Lower-left: ReO3 single-crystals. Right: The jungle-gym Fermi surface with arrows and cross-sectional planes representing the applied field directions.

S. Liang, et al. A gap-protected zero-Hall effect state in the quantum limit of the non-symmorphic metal KHgSb. Nature Materials 18, 443–447 (2019).
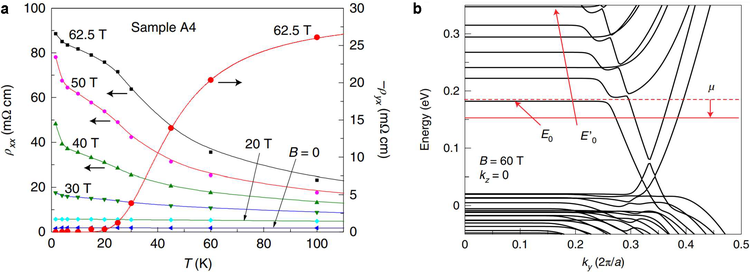
- A recurring theme in topological matter is the protection of unusual electronic states by symmetry, for example, protection of the surface states in Z₂ topological insulators by time-reversal symmetry. KHgSb is predicted to exhibit double quantum spin Hall states, protected by non-symmorphic (glide) symmetry. In strong magnetic fields B up to 62.5 T, we found that KHgSb enters a state with large magnetoresistance but zero Hall resistivity (in a normal metal this would increase linearly with B). We proposed that, in this quantum limit, the chemical potential drops into the bulk gap, intersecting equal numbers of right- and left-moving quantum spin Hall surface modes to produce the zero-Hall state.

KHgSb Zero-Hall state — Zero-Hall state in KHgSb. a. Divergent behaviours of the Hall resistivity ρyx (red circles) and resistivity ρxx (symbols) in the LLL. As T→ 2 K, ρxx increases steeply, implying a sharp decrease of the itinerant population. Paradoxically, the Hall resistivity ρyx (a negative quantity) plunges to 0 below 20 K instead of diverging to very large values as expected from loss of itinerant carriers. These opposite trends imply a surface conduction channel in parallel with the bulk (see text). The saturation of ρxx at 62 T as T→ 2 K also constitutes evidence for the surface conduction mode. The solid red curve is a fit to ρyx using equation (1); the curves drawn through the ρxx symbols are guides to the eye. b. The LL spectrum in B= 60 T with zigzag termination on a (100) surface. In the conduction band, all LLs disperse upwards at the surface except for the lowest LL (at energy E0 ~ 0.18 eV) and its partner produced by band folding at kz=π/c at energy E′ 0 ~ 0.35 eV, which disperse downwards to form a pair of left-moving QSH states. Conversely, a pair of right-moving QSH states emerge from the valence band. In the quantum limit, magnetic freeze-out lowers μ into the gap (dashed line to solid) where it intersects two left- and two right-moving QSH modes to give σxy= 0.

S. Liang, et al. Experimental Tests of the Chiral Anomaly Magnetoresistance in the Dirac-Weyl Semimetals Na₃Bi and GdPtBi. Physical Review X 8, 031002 (2018).
- In the 3D Dirac-Weyl semimetal, the chiral anomaly appears as an “axial” current arising from charge pumping between the lowest (chiral) Landau levels of the Weyl nodes, when an electric field is applied parallel to a magnetic field B. Evidence for the chiral anomaly was obtained from the longitudinal magnetoresistance (LMR) in Na₃Bi and GdPtBi. However, current-jetting effects (focusing of the current density J) raised general concerns about LMR experiments. Here, we implemented a litmus test that allows the intrinsic LMR in Na₃Bi and GdPtBi to be sharply distinguished from pure current-jetting effects. These results considerably strengthen the evidence for the intrinsic nature of the chiral-anomaly-induced LMR.

Chiral anomaly — (a) The Landau spectrum of Weyl fermions. In a field B ∥ x, the lowest Landau levels are chiral with velocity v either ∥ B or −B. Application of E ∥ B transfers charge between them, which increases the left-moving population NL at the expense of the right-moving population NR (the bold blue and red curves indicate occupations of the LLs). Panel (b) shows a pair of voltage contacts (blue dots) placed on the line joining the current contacts (white circles). A second pair (yellow) is placed along an edge. Panel (c) is a schematic drawing of the intensity map of Jx (with dark regions being the most intense) when current-jetting effects are pronounced. The profile of Jx vs y (with x at the dashed line) is sketched on the right.

T. Liang, et al. Anomalous Hall effect in ZrTe₅. Nature Physics 14, 451–455 (2018).
- The anomalous Hall effect (AHE) normally only occurs in ferromagnetic metals where the magnetic ions contribute an additional magnetization-dependent term to the Hall resistance at zero field. In this paper, we found a large AHE signal in a topological (Dirac) semimetal that is completely non-magnetic. Through a series of precise double-axis rotation experiments, we mapped out how the Berry curvature of the Dirac nodes generates this unconventional AHE.

Magnetotransport in ZrTe5. H lies within the ab plane at selected θ (inset). a, Variations of ρxx versus H at selected θ. Negative LMR is observed in a small angular regime θ≲θ≲1°. b, Hall data at selected θ reveal a highly unusual zigzag pattern that suggests a dominant anomalous Hall contribution. c, Full angular dependence of the anomalous Hall contribution ρ0AHE obtained from d. The upper right inset shows ρ0AHE at small angles and the lower left inset shows the angular dependence of the background slope. d, ρAHE after removal of the high-field linear background (the ordinary Hall term) from the curves in b. At fixed θ, the AHE curves are antisymmetric with respect to H. However, plotted as a function of θ (c), ρAHE is distorted by a large, in-plane Hall contribution acquired by a slight misalignment.

And many more. Find them here.